Integer Arithmetic Made Easy
SHRAVAN S K
Aug 21, 2021
Integer arithmetic is a tricky area for many students as they struggle to make sense of why and how the rules have come about. To subtract a negative integer from another negative integer, for example , the steps or rules to be followed could be:
| (i) Two negative signs becomes positives (for some unknown reason) | Change |
| (ii) To add a positive integer and a negative integer, take the difference of the two numbers ignoring the signs and assign the symbol corresponding to the larger of the two numbers again ignoring the signs (for some unknown reason) | (-3) + (+5) 5 - 3 = 2 +2 Hence, (-3) - (-5) = +2 |
What impact does giving rules like these without context or justification has on students?
Confusion, lack of appreciation towards math and possibly hatred towards the subject. Of course students tend to come to terms with such rules over time, by memorising the rules & repeatedly applying them blindly in multiple exercise problems, without a proper understanding.
This is a topic even many teachers find it hard to take forward to their students. Here, we present integer addition & subtraction using a definition of zero(not just as a number or a placeholder) which makes it easily accessible & understandable.
(+7) + (+4) is 4 positives added to 7 positives.

We start redefining how we communicate, say 7 + 4. Instead of Four added to seven” or “Positive four added to positive seven”, we can say “Four positives added to seven positives” which gives eleven positives(+11).
| (+1) + (+2) = (+3) | (+7) + (+20) = (+27) | (+358) + (+1098) = (+1456) | (+a) + (+b) = +(a + b) |
Also, (+7) - (+4) would be “Four positives removed/subtracted from Seven positives” which gives +3.
| (+2) - (+1) = (+1) | (+20) - (+7) = (+13) | (+1098) - (+358) = (+740) | (+a) - (+b) = +(a - b), where a > b |
Let’s try with negative numbers. What would (-7) + (-4) mean? Yes, add 4 negatives to 7 negatives which gives 11 negatives (-11).
| (-2) + (-1) = (-3) | (-7) + (-20) = (-27) | (-1098) + (-358) = (-1456) | (-a) + (-b) = -(a + b) |
(-7) - (-4) is 4 negatives removed from 7 negatives.

Now, let us try (-7) - (-4). This means to remove four negatives from seven negatives which results in 3 negatives (-3).
| (-2) - (-1) = (-1) | (-20) - (-7) = (-13) | (-1098) - (-358) = (-740) | (-a) - (-b) = -(a - b), where a > b |
(+4) - (+7) is 7 positives removed from 4 positives.
Looks good so far! What if we did (+4) - (+7) i.e. “Remove seven positives from four positives”?
Everything seems to break! How can we remove something more than what is present?!
Can you find some more of these examples?
You may have come up with examples like:
| (+1) - (+2) | (+7) - (+20) | (+358) - (+1098) | (+a) - (+b), where a < b |
Are there any other types of such examples? Try and find out.
Yes, the same happens with negative numbers as well. (-4) - (-7) where we should remove 7 negatives from 4 negatives!
| (-1) - (-2) | (-7) - (-20) | (-358) - (-1098) | (-a) - (-b), where a < b |
If you thought you have found out all, you are in for a surprise. There are some more.
How about (+4) - (-7), which is to remove 7 negatives from 4 positives; sounds even more ridiculous.
| (+1) - (-2) | (+20) - (-7) | (+358) - (-1098) | (+a) - (-b) |
There is one more: (-4) - (+7) i.e. remove 7 positives from 4 negatives; sounds equally ridiculous as the previous one.
| (-1) - (+2) | (-20) - (+7) | (-358) - (+1098) | (-a) - (+b) |
(-3) + (+4) 4 positives added to 3 negatives.

There are also operations like, (-3) + (+4) which means, adding 3 negatives and four positives where simplifying it further is not straightforward.
| (-1) + (+2) | (+7) + (-20) | (+358) + (-1098) | (+a) + (-b) or (-a) + (+b) |
How can we make sense of these operations? What meaning could they have?
Well, nothing to worry about; zero comes to our rescue here. Yes, you read it right. ZERO.
Zero can be defined as “Any number removed from itself”. For example,
| (+15) - (+15) = 0 | (+a) - (+b) = 0, where a = b | (-15) - (-15) = 0 | (-a) - (-b) = 0, where a = b |
Any number removed from itself is Zero.
Sum of equal positives and negatives is Zero.

Zero can also be defined as “The sum of equal positives and negatives”; which means each positive is equal and opposite to a negative. For example,
| (+15) + (-15) = 0 | (+a) + (-b) = 0, where a = b | (-15) + (+15) = 0 | (-a) + (+b) = 0, where a = b |
Different analogies can be attached to the positives and negatives -> Positrons & Electrons, Assets & Debts, Births & Deaths, Profit & Loss etc. Some artificial analogies can also be used here. For example, Two teams of same sized and equally capable robots playing tug of war. A physical balancing scale where equal quantities of unit weights are placed on both the sides. In these analogies, the game of tug of war and the physical scale would remain intact/balanced at the starting position irrespective of the quantity on both sides given it is equal on either side.
That’s all okay, but how can we use Zero to evaluate the seemingly weird operations we saw?!
Let’s start with (-3) + (+4) -> we have 3 negatives and 4 positives. Using the
- Definition of zero being equal amounts of positives and negatives
we can form 3 pairs of positives and negatives making this 0 and we will be left with 1 positive. So, (-3) + (+4) = (+1).
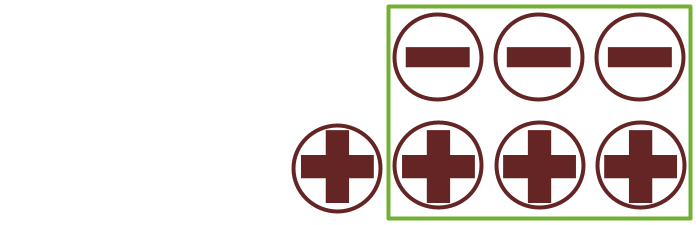
Continuing this, can you try solving for (-4) + (+3)? How many pairs can we make out of 4 negatives and 3 positives? Yes, that would be 3 pairs which would make this zero. Now, we are left with 1 negative. So, (-4) + (+3) = (-1).
| (-1) + (+2) = (+1) | (+7) + (-20) = (-13) | (+358) + (-358) = 0 | (+a) + (-b) = +(a - b) [a>b] (+a) + (-b) = -(b - a) [b>a] (-a) + (+b) = -(a - b) [a>b] (-a) + (+b) = +(b - a) [b>a] |
| (-2) + (+1) = (-1) | (+20) + (-7) = (+13) | (-1098) + (+1098) = 0 |
Easy-peasy, don’t you think?!
Let’s try (+4) - (+7). We are supposed to remove 7 positives from 4 positives, but to successfully complete this we are falling short of 3 positives. We know that if we don’t add anything to a number(or add 0) its value doesn’t change. For example,
| (+15) + 0 = (+15) | (+a) + 0 = (+a) | (-15) + 0 = (-15) | (-a) + 0 = (-a) |
(The same is true with subtraction also)
We also know that equal amounts of positives and negatives make zero. Can we use these two facts to make up for the shortfall of 3 positives for performing (+4) - (+7)? Yes! We can add 3 pairs of positives & negatives to (+4) which makes it 7 positives & 3 negatives.
But, remember that the value has not changed as we have just added a zero.
Now, we are supposed to remove 7 positives from this which will result in 3 negatives or (-3). So, (+4) - (+7) = (-3). Voila! Experience the power of nothingness(ZERO)!!
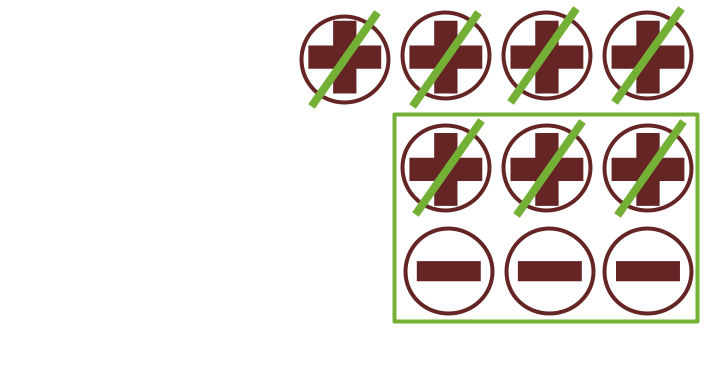
| (+1) - (+2) = (-1) | (+7) - (+20) = (-13) | (+358) - (+1098) = (-740) | (+a) - (+b) = -(b - a), where a < b |
(-4) - (-7) 7 negatives removed from 4 negatives
Try for (-4) - (-7). To remove 7 negatives from 4 negatives, there would be a shortfall of 3 negatives. So, we can add 3 pairs of positives and negatives and after taking out 7 negatives we would be left with 3 positives; which means (-4) - (-7) = (+3).
| (-1) - (-2) = (+1) | (-7) - (-20) = (+13) | (-358) - (-1098) = (+740) | (-a) - (-b) = +(b - a), where a < b |
(+4) - (-7) 7 negatives removed from 4 positives
How about (+4) - (-7)? We have 4 positives and we are supposed to remove 7 negatives which is a shortfall of 7 negatives. How many pairs should we add here? 7 pairs of positives and negatives. Now, we have 11 positives and 7 negatives from which 7 negatives are to be removed. So, (+4) - (-7) = (+11)
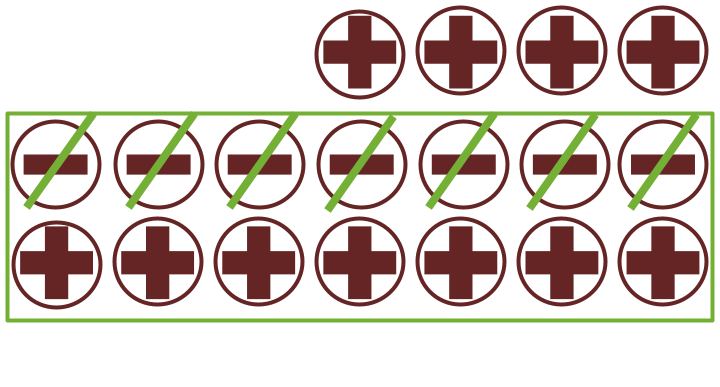
| (+2) - (-1) = (+3) | (+20) - (-7) = (+27) | (+358) - (-1098) = (+1456) | (+a) - (-b) = +(a + b) |
Try (-4) - (+7). To remove 7 positives from 4 negatives, there would be a shortfall of 7 positives. So, we can add 7 pairs of positives and negatives. Now, we have 7 positives and 11 negatives from which 7 positives are to be removed. So, (-4) - (+7) = (-11).
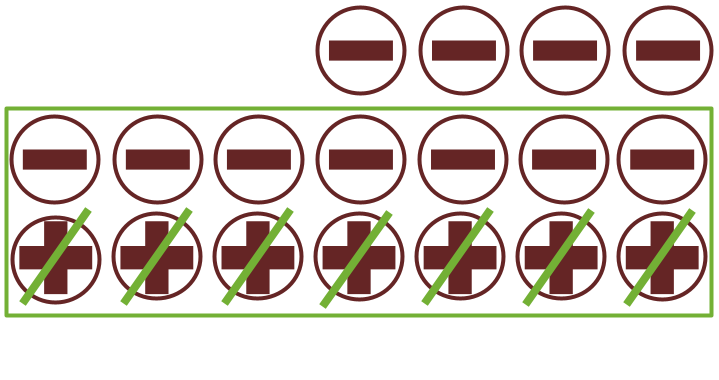
| (-2) - (+1) = (-3) | (-20) - (+7) = (-27) | (-358) - (+1098) = (-1456) | (-a) - (+b) = -(a + b) |
We have covered all cases of integer addition and subtraction. How did you find it? Do you think this can be taken forward to classrooms?
I feel this way of introduction is easily understood and appreciated. Also, here the rules can be discovered and arrived at as part of the exploration. There is no burden of remembering the rules.
Here is a puzzle for you based on what we have gone through so far. Give it a shot.
Hint: Give away the highest debt container in exchange for the highest asset container.
This work is adapted and improvised from the idea of Zero given by Brahmagupta. They also address multiplication of integers.